数据结构与算法 | 面试总结

Posted on | In |

数据结构

栈

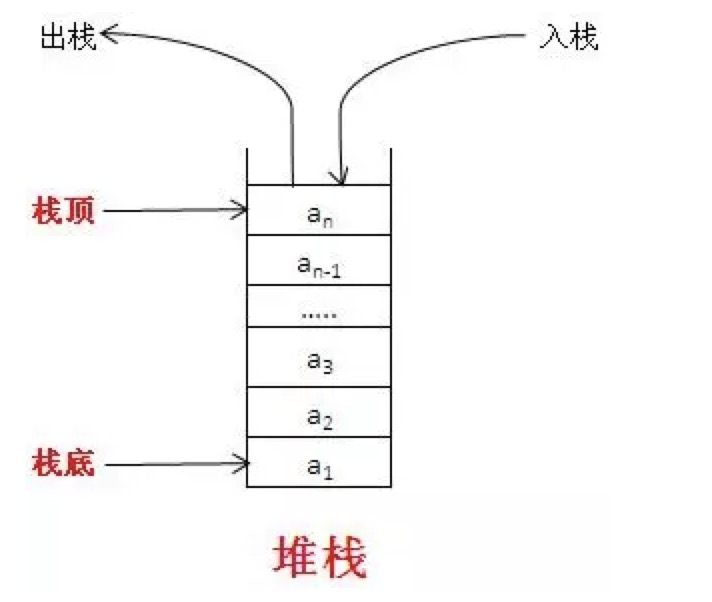
栈是一种特殊的列表，栈内的元素只能通过列表的一端访问，这一端称为栈顶。想象一下，我们平常在饭馆见到的一摞盘子就是现实世界常见的栈的例子，只能从最上面取盘子，盘子洗干净后，也只能放在最上面。栈被称为一种后入先出的数据结构。是一种高效的数据结构，因为数据只能在栈顶添加或删除，所以这样的操作很快。 使用条件：

只要数据的保存满足后入先出或先进后出的原理，都优先考虑使用栈

栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function Stack() {
  var items = [];
  this.push = function(element){//添加一个（或几个）新元素到栈顶
    items.push(element);
  };
  this.pop = function(){//移除栈顶的元素，同时返回被移除元素
    return items.pop();
  };
  this.peek = function(){//返回栈顶的元素，但并不对栈做任何修改
    return items[items.length-1];
  };
  this.isEmpty = function(){//如果栈内没有任何元素就返回true，否则返回false
    return items.length == 0;
  };
  this.size = function(){//返回栈里的元素个数
    return items.length;
  };
  this.clear = function(){//移除栈里的所有元素
    items = [];
  };
  this.print = function(){//打印
    console.log(items.toString());
  };
  this.toString = function(){
    return items.toString();
  };
}

队列

队列也是一种列表，不同的是队列只能在队尾插入元素，在队首删除元素。想象一下，我们在银行排队，排在最前面的人第一个办理业务，而后面来的人只能排在队伍的后面，直到轮到他们为止。 使用条件：

只要数据的保存满足先进先出、后入后出的原理，都优先考虑使用队列
常见应用场景：

队列主要用在和时间有关的地方，特别是操作系统中，队列是实现多任务的重要机制
消息机制可以通过队列来实现，进程调度也是使用队列来实现

队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function Queue() {
  var items = [];
  this.enqueue = function(element){//向队列尾部添加一个（或是多个）元素
    items.push(element);
  };
  this.dequeue = function(){//移除队列的第一个元素，并返回被移除的元素
    return items.shift();
  };
  this.front = function(){//返回队列的第一个元素——最先被添加的,也将是最先被移除的元素。队列不做任何变动。（不移除元素，只返回元素信息。与stack的peek方法类似）
    return items[0];
  };
  this.isEmpty = function(){//如果队列内没有任何元素就返回true，否则返回false
    return items.length == 0;
  };
  this.clear = function(){//移除队列里的所有元素
    items = [];
  };
  this.size = function(){//返回队列里的元素个数
    return items.length;
  };
  this.print = function(){//打印                                                                                                                                                                                                                             
    console.log(items.toString());
  };
 }

链表

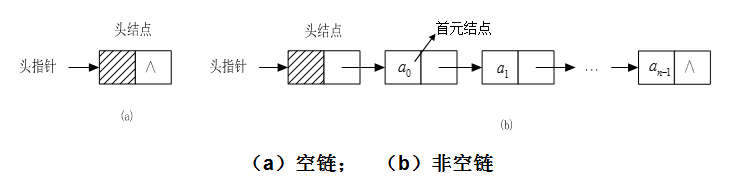
链表也是一种列表，为什么需要出现链表，JavaScript中数组的主要问题时，它们被实现成了对象，与其他语言（比如C++和Java）的数组相对，效率很低。如果你发现数组在实际使用时很慢，就可以考虑使用链表来代替它。 使用条件：

链表几乎可以用在任何可以使用一维数组的情况中。如果需要随机访问，数组仍然是更好的选择。

链表

二叉树和二叉查找树

  • 树是计算机科学中经常用到的一种数据结构。
  • 树是一种非线性的数据结构，以分层的方式存储数据。
  • 二叉树每个节点的子节点不允许超过两个。一个父节点的两个子节点分别称为左节点和右节点，通过将子节点的个数限定为2，可以写出高效的程序在树中插入、查找和删除数据。
  • 二叉查找树（BST）是一种特殊的二叉树，相对较小的值保存在左节点中，较大的值保存在右节点中。这一特性使得查找的效率很高，对于数值型和非数值型的数据，比如单词和字符串，都是如此。

二叉查找树实现方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
function Node(data, left, right) { // 创建节点
  this.data = data;
  this.left = left;
  this.right = right;
  this.show = show
}
function show () { // 显示树的数据
  return this.data
}
function BST () { // 二叉查找树类
  this.root = null;
  this.insert = insert;
  this.inOrder = inOrder; // inOrder是遍历BST的方式
}
function insert (data) { // 向树中插入数据
  var n = new Node(data, null, null)
  if (this.root == null) {
    this.root = n;
  } else {
    var current = this.root;
    var parent;
    while (true) {
	  parent = current
	  if (data < current.data) {
		current = current.left;
		if (current == null) {
		  parent.left = n;
		  break;
		}
	  } else {
		current = current.right;
		if (current == null) {
		  parent.right = n;
		  break;
		}
	  }
    }
  }
}

时间复杂度

一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数f(n)，算法的时间度量记为 T(n) = O(f(n)) ，它表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称时间复杂度。这里需要重点理解这个增长率。

举个例子，看下面3个代码：

1、{++x;}

2、for(i = 1; i <= n; i++) { ++x; }

3、for(j = 1; j <= n; j++)
for(j = 1; j <= n; j++)
{ ++x; }

上述含有 ++x 操作的语句的频度分别为1 、n 、n^2，

假设问题的规模扩大了n倍，3个代码的增长率分别是1 、n 、n^2

它们的时间复杂度分别为O(1)、O(n )、O(n^2)

二分查找

  • 二分查找的时间复杂度为O(logn)

规则

  • 定义最小索引和最大索引
  • 计算出中间索引
  • 拿中间的索引和要查找元素的索引进行比较
  • 相等:就返回当前的中间索引
  • 不相等:
    • 如果大了:在左边查找,max = min - 1
    • 如果小了:在右边查找,min = min + 1 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * 二分查找，递归实现。
 * @param target 目标数字
 * @param arr  原数组
 * @param start 开始的地方
 * @param end 结束的地方
 * @returns {*}
 */
function binarySearch(target,arr,start,end) {
    var start   = start || 0;
    var end     = end || arr.length-1;
    var mid = parseInt(start+(end-start)/2);
    if(target==arr[mid]){
        return mid;
    }else if(target>arr[mid]){
        return binarySearch(target,arr,mid+1,end);
    }else{
        return binarySearch(target,arr,start,mid-1);
    }
    return -1;
}
/**
 * 有序的二分查找，返回-1或存在的数组下标。不使用递归实现。
 * @param target
 * @param arr
 * @returns {*}
 */
function binarySearch(target,arr) {
    var start   = 0;
    var end     = arr.length-1;
    while (start<=end){
        var mid = parseInt(start+(end-start)/2);
        if(target==arr[mid]){
            return mid;
        }else if(target>arr[mid]){
            start = mid+1;
        }else{
            end = mid-1;
        }
    }
    return -1;
}

排序

1
2
3
4
5
6
7
let len = array.length
swap = (array, index1, index2) => {
  let temp = array[index2]
  array[index2] = array[index1]
  array[index1] = temp
}

冒泡

  • 从第一个数字开始，依次往后对比，直到最后一位，当该数字大于/小于查找位置上数字时，交换数字
  • 重新一轮开始时，对比直到倒数第二位
1
2
3
4
5
6
7
for (let i = 0; i < len; i++) {
  for (let j = 0; j < len - i; j++) {
    if (array[j] > array[j + 1]) {
      swap(array, j, j + 1)
    }
  }
}

选择排序

  • 与冒泡相似
  • 从第一位开始，依次对比找到最小那一位，存下下标，与第一位做交换
  • 从第二位开始，再次找最小那一位
1
2
3
4
5
6
7
8
9
10
11
12
13
let min
for (let i = 0; i < len; i++) {
  min = i
  for (let j = i + 1; j < len; j++) {
    if (array[min] > array[j]) {
      min = j
    }
  }
  if (min != i) {
    swap(array, i, min)
  }
}

插入排序

  • 将组分成“已排序”和“未排序”
  • 从第一位开始，依次从“未排序”获取一位，再对“已排序”列表进行排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 方案一
for (let i = 0;i < len; i++) {
  for (let j = i;j > 0;j--) {
    if (array[j] > array[j - 1]) {
      swap(array, j, j - 1)
    }
  }
}
// 方案二：以下方法可以减少交换次数
for (let i = 0; i < len; i++) {
  let value = array[i]
  for (let j = i; j >= 0; j--) {
    if (array[j - 1] > value) {
      array[j] = array[j - 1]
    } else {
      array[j] = value
      break
    }
  }
}

归并排序/分治法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function mergeSort(arr) {
  if (arr.length <= 1) return arr;
  let middle = parseInt(arr.length / 2)
  let left = arr.slice(0, middle)
  let right = arr.slice(middle)
  if (!left || !right) {
    return false;
  }
 return merge(mergeSort(left), mergeSort(right))
}
function merge(left, right) {
  let result = []
  while (left.length && right.length) {
    if (left[0] <= right[0]) {
      result.push(left.shift())
    }
    else {
      result.push(right.shift())
    }
  }
  while (left.length) {
    result.push(left.shift())
  }
  while (right.length) {
    result.push(right.shift())
  }
  return result
}

参考：JavaScript排序算法（二）——归并排序

快速排序

取中间值，然后不断比较左右两边的数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var quickSort = function(arr) {
  　　if (arr.length <= 1) { return arr; }
  　　var index = parseInt(arr.length / 2);
  　　var pivot = arr[index];
  　　var left = [];
  　　var right = [];
  　　for (var i = 0; i < arr.length; i++) {
  　　　　if (arr[i] < pivot) {
  　　　　　　left.push(arr[i]);
  　　　　} else {
  　　　　　　right.push(arr[i]);
  　　　　}
  　　}
  　　return quickSort(left).concat([pivot], quickSort(right));
  };